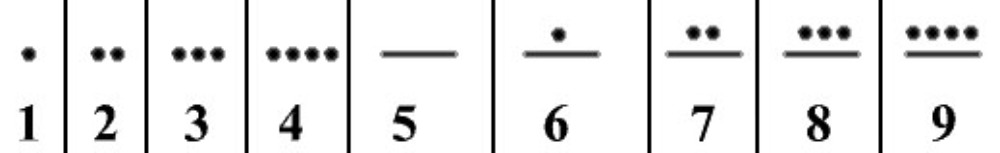Numblers: cuentas claras para los niños

A lo largo de la historia, los sistemas de representación numérica han ido evolucionando hasta formas cada vez más abstractas. En la actualidad, el sistema de raíz indo-arábigo es utilizado casi universalmente. Sin embargo, la manera en que los niños lo aprenden y trabajan dificulta la comprensión de sus propiedades y operaciones. En este artículo vamos a analizar algunos sistemas de representación y vamos a proponer un sistema de bloques combinables que física y visualmente sirve para ayudar a entender propiedades y operaciones numéricas. El proyecto, llamado «Numblers», ha ganado el primer premio en el concurso «Ciencia en Acción» organizado por el CSIC, ICMAT y UNED, entre otros.

Situación de partida. Definición del problema.

Nada en la representación visual (significante) del número «3», por poner un ejemplo, indica que es lo mismo que 2+1 o que 1+1+1. Esto no era así en el sistema de representación romano en el que el «3» se representaba como «III» cuyo significado es mucho más explícito; su significante es indicativo de su significado. Éste será nuestro primer punto de partida.

Los números romanos, por razones prácticas conocidas, fueron sustituidos por los indo-arábigos. Por ejemplo, los números grandes son más fáciles de crear ya que con muchos menos signos (sólo diez) se puede crear fácilmente cualquier número. Pero lo que se ganó en versatilidad como sistema (porque es más fácil y rápido operar con ellos) y posibilidades de cálculo fue a base de una abstracción que hace su comprensión mucho menos intuitiva; sobre todo al principio de su aprendizaje. Cuando los niños aprenden la serie del uno al diez, no entienden que están sumando una unidad al número anterior. Para aprehender algo es mucho mejor poder manipular, experimentar, observar y crear con el fenómeno objeto de estudio. Pero, ¿cómo podemos hacer que un niño manipule, observe y juegue con algo tan abstracto como los números para que los entiendan mejor? Todos hemos empezado a entender los números, la suma y la resta contando con los dedos. Si ha funcionado durante tanto tiempo a tantas personas su eficacia está probada. Pero no podemos evitar las siguientes preguntas:

• ¿Podríamos encontrar una forma igual de eficaz pero más útil? Recordemos que solo tenemos 20 dedos.

• ¿Podríamos encontrar algo un poco mejor diseñado para que comunique mejor el significado y las propiedades de los números, que sea abierto y accesible a todos?

Nuestro problema es encontrar un sistema de representación numérico que permita a los niños pequeños una comprensión profunda de los números y sus propiedades, y que sirva de base para seguir aprendiendo de forma coherente, con dicho sistema, propiedades cada vez más complejas.

Elementos del problema

En este apartado vamos a dividir nuestro problema en aquellos problemas menores de los cuales está compuesto. Según nuestras observaciones, los pequeños no entienden entre otras cosas:

• Que cuando cuentan, están sumando una unidad al número anterior.

• Que un mismo número puede ser suma de varios diferentes.

• La propiedad conmutativa.

• Saben realizar operaciones pero les cuesta saber utilizarlas.

• La divisibilidad.

• Los números negativos.

• Las fracciones.

• Las potencias al cuadrado.

Recopilación de datos

Para encontrar referencias anteriores que puedan servir como base para la solución de este problema hemos realizado una recopilación de diferentes sistemas de representación numérica hasta nuestros días. Todos, excepto el índigo-arábigo utilizan el principio de adición. Aquí mostramos un resumen:

• Numerales arameos o aramaicos

  

• Operaciones con los dedos

  

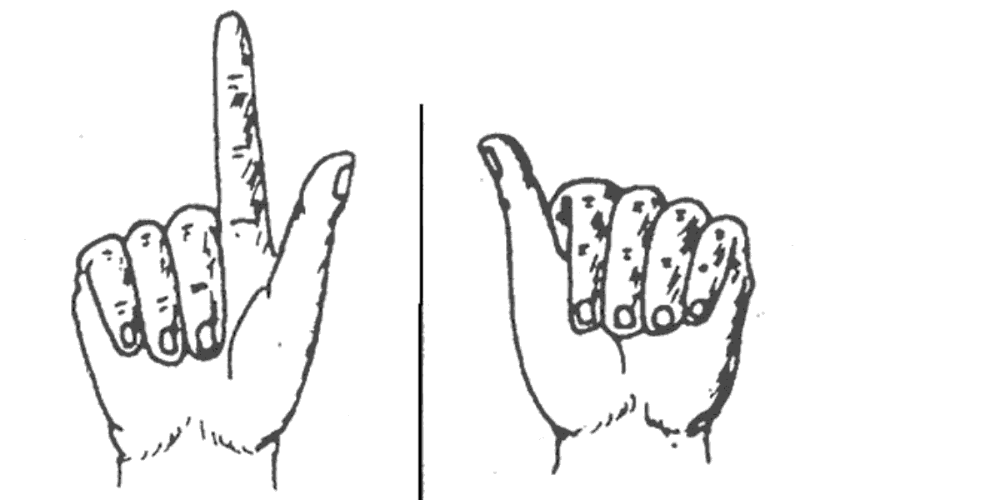
• Sistema de cinco barras
  ​

  

• Numerales en Creta​

  

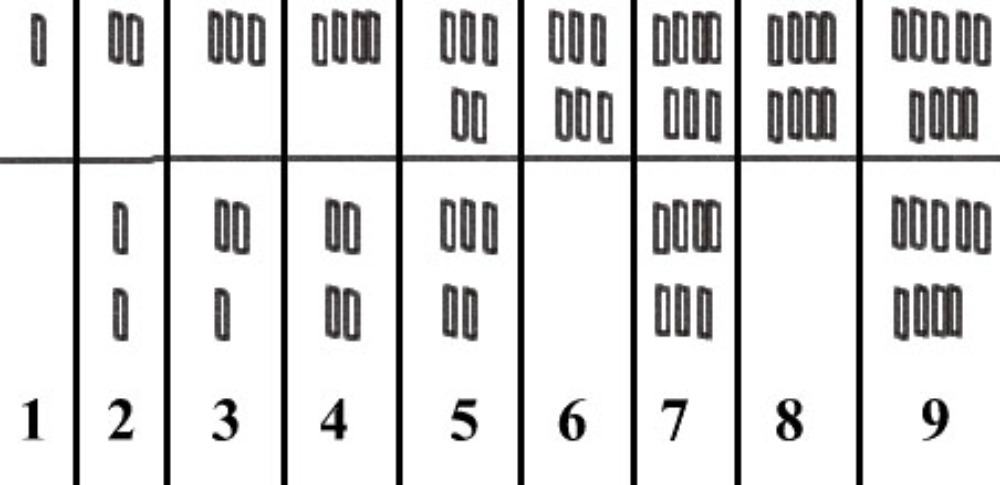
• Numerales mayas

  

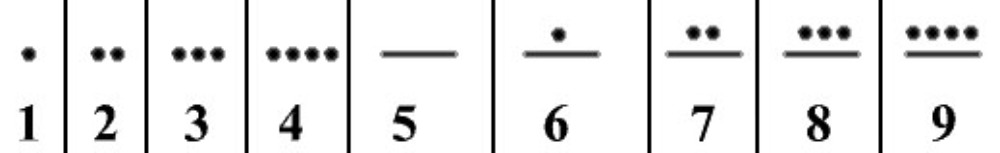
• Numerales romanos

  

• Numerales índigo-arábigos

  

Análisis de datos.

Lógicamente, el sistema que más se analizará y el que servirá mejor de base es el de Numicon del que presentamos una imagen a modo de resumen de sus características.

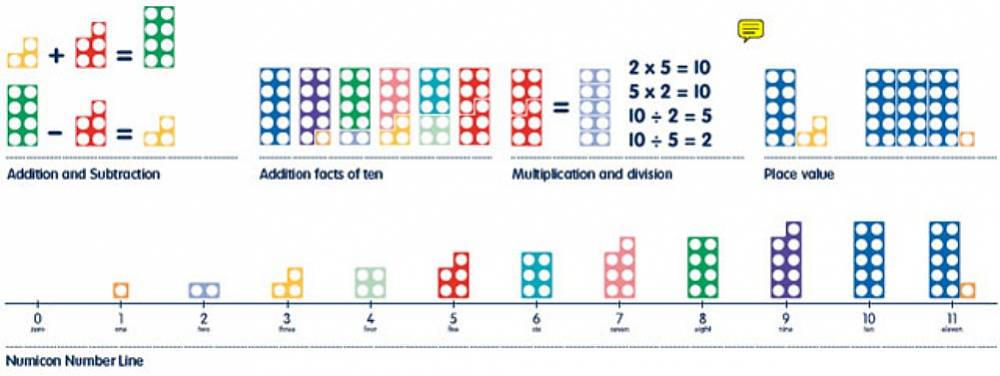
Las características más interesantes que encontramos son:

• Por su forma, se ve intuitivamente, que un número es igual a su anterior más uno.

• Por su forma también, cuando se suman o restan números pequeños, la forma resultante es la misma que la del número que sale como resultado.

• Los agujeros perforados en la pieza de plástico lo hacen muy manejable para los dedos de los niños y permite que se apilen. Además, el recurso de los dedos les sirve para contar también con ellos.

Sin embargo, para la operación de restar no existe un proceso claro. Algunas veces se hace introduciendo los dedos en los agujeros para taparlos —lo cual es un poco confuso— y también se ofrecen por Internet plantillas de papel para tapar los agujeros, lo cual hace que el sistema pierda coherencia.

Por otro lado tampoco encontramos que el sistema sea lo suficientemente abierto como para poder servir para las divisiones, los números negativos, etc. En nuestra opinión, parece que con la idea de que al sumar la forma resultante sea la misma que la del número del resultado, y la de que se entiendan bien los números pares e impares, se han sacrificado otras posibilidades para que el modelo explique más propiedades de los números.

Por último, este sistema siempre requiere la presencia de un adulto para plantear los problemas. Está pensado para ayudar a los profesores con los alumnos, pero esto le resta interés como juego para que los niños se diviertan —y aprendan— autónomamente.

Creatividad

Con el objetivo de crear un sistema coherente con muchas más propiedades numéricas y útil para entenderlas de forma visual y física proponemos:

• Tener como base un cuadrado relleno de color (sin orificios) para los números positivos.

• Un cuadrado negro con borde del mismo color que el positivo para los números negativos.

• Formas que expresen la divisibilidad y las potencias (al cuadrado).

• Fracciones del cuadrado base para representar las fracciones y el concepto de infinitesimal.

En general, se ha buscado que el sistema sea capaz de ofrecer un sencillo mapa mental o modelo conceptual completo para que los niños puedan entender mejor el significado de los números, sus propiedades y las operaciones aritméticas básicas. Un modelo conceptual que les sirva de base para buscar su propia forma de entender los números y las operaciones jugando y utilizándolo para no enfrentarse desnudos a entes tan abstractos. Si para no enfrentarse a entes tan abstractos deciden utilizar los dedos, este sistema es un poco más útil, mucho más completo y mucho menos limitado.

Experimentación

El sistema ha sido probado en niños de 4 y 5 años que han sido capaces de resolver problemas de suma, resta, multiplicación y división. Algunos tipos de problema resueltos en las pruebas han sido:

• Este sistema ha sido utilizado por un niño de 5 años para hacer divisiones de un número de juguetes (12) para diferentes números de niños (3, 4, 6, etc.). Otro tipo de problema resuelto era averiguar cuántas ruedas son necesarias para montar x motos. También era muy ilustrativo ver cómo entendían las propiedades conmutativa y asociativa simplemente «montando» el mismo número de varias formas o con varias piezas diferentes.

• Entender mejor las tablas de multiplicar y las series numéricas.

• Además, al partir de un concepto tan abierto, los niños, los profesores o los padres siempre pueden plantearse ampliar el sistema.

 

El sistema se puede descargar para imprimir.

Más información

¿Qué te pareció? ¡Comparte tu opinión ahora!

---

---

Este video podría interesarte👇👇👇