(Des)orden en el espacio
Los fundamentos geométricos de Critchlow como herramienta para el proceso creativo del diseño.
- Opiniones:
- 3
- Votos:
- 37
G. Bachelard (1991) nos dice que para construir el pensamiento científico es necesario llevar a cabo un proceso lógico de abstracción, tarea que encaja a la perfección con lo que el diseño gráfico pretende: pasar de la imagen (mental) a la forma geométrica y de ella a la forma abstracta, con la finalidad de generar el consenso que busca el trabajo de diseño. De esta manera el diseñador se encargaría de dibujar y traducir lo concreto a lo abstracto por medio del trazo geométrico, puente entre lo experiencial-empírico y lo científico-matemático.
Para lograrlo, se requieren ciertos fundamentos que son comúnmente ignorados por los profesionales que intervienen en el proceso creativo; procesos que ayudan a pasar de una etapa meramente imaginativa a una construcción formal adecuada. R. Scott (1970: 7-8) estableció un proceso general que debería seguir todo diseño. Lo enmarca en cuatro «causas» básicas.1 Este mismo autor menciona, además, dos tipos de relaciones visuales que se deben contemplar como condiciones necesarias para elaborar una propuesta: la primera de ellas es determinar si lo diseñado será bidimensional, tridimensional o tendrá relaciones de espacio y tiempo (producto audiovisual). El diseño de un signo, cuando menos para su conceptualización y construcción inicial, se ubicará en el plano bidimensional. A esta delimitación Scott la denomina como «relación visual». Otro tipo de relación es la «estructural», que es lo que le da coherencia y unidad a lo diseñado pero que, sin embargo, resulta más difícil de comprender y aplicar, porque generalmente no se encuentra en la esfera de lo visible.
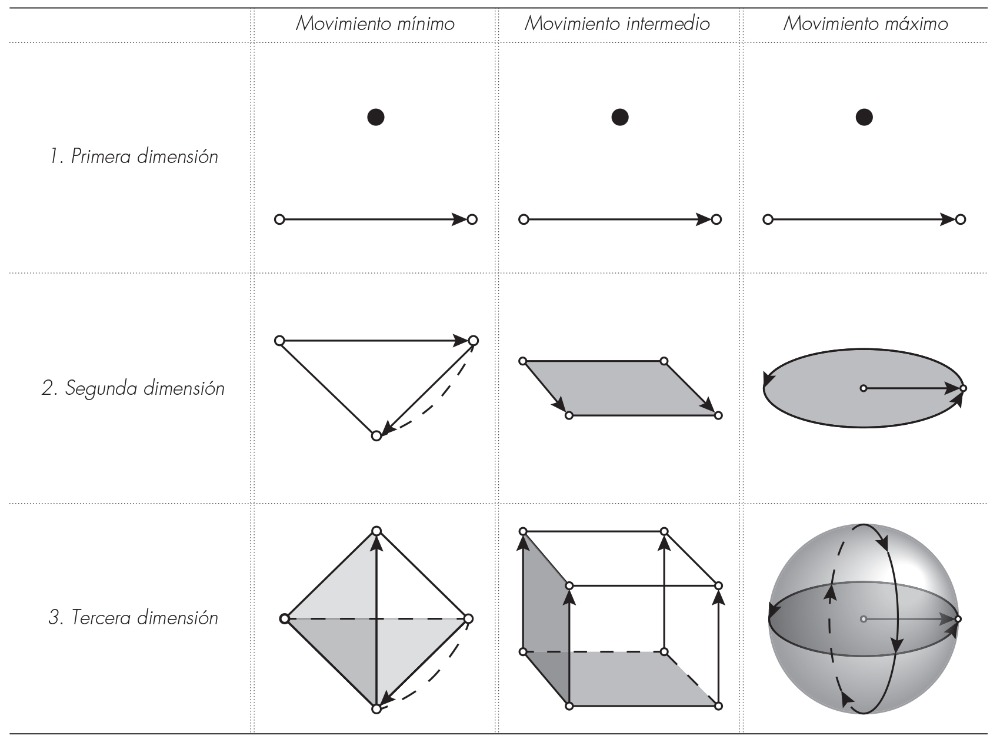
K. Critchlow, renombrado arquitecto inglés (nacido en 1933), toma como la unidad básica de todo diseño al punto y los movimientos que este realiza a través de un determinado espacio bi y tridimensional; el punto es conceptualmente relativo, pues depende de la experiencia humana. Un punto describe algunos volúmenes primarios por medio de su traslado en el espacio.2
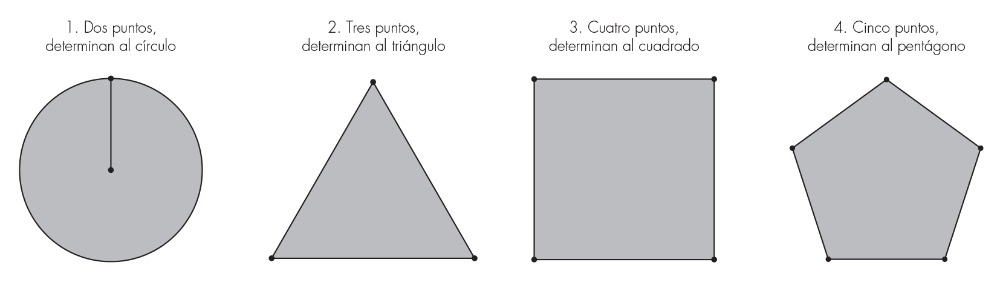
En diseño, toda forma básica tiene un fundamento geométrico, y su conocimiento objetivo nos permite explorar creativamente algunas derivaciones que pueden realizarse, ya sea desde su propia construcción con base en elementos básicos de diseño (la unión de puntos), o mediante la interrelación de formas básicas. El triángulo, el cuadrado y el pentágono están directamente relacionados con los primeros tres sólidos platónicos: el tetraedro se forma de triángulos, el octaedro puede ser visto como tres cuadrados intersecados, mientras que el arreglo pentagonal de puntos —junto con sus propiedades áureas— es la característica del icosaedro (Critchlow, 2000: 58).3
El uso de sistemas estructurales debería ser considerado como una de las partes fundamentales para la elaboración de un diseño, pues es a través de un ordenamiento espacial de módulos como se le dará coherencia formal a las propuestas de diseño.
«Casi todos los diseños tienen una estructura […] La estructura es la disciplina que subyace bajo tales disposiciones [...] La estructura puede ser formal, semiformal o informal. Puede ser activa o inactiva. También puede ser visible o invisible».
Las estructuras formales se componen de líneas estructurales que aparecen de manera rígida y matemática, ayudan a la formación completa del diseño. El espacio bidimensional de estas redes queda subdividido en una cantidad igual y rítmica. Dentro de las estructuras formales, podemos encontrar a las estructuras regulares, conformadas por las tres formas básicas: el triángulo, el cuadrado y el hexágono.4
W. Wong (2004) describe otro tipo de estructuras, y las llama de «múltiple repetición». Estas se construyen también por patrones geométricos regulares. Critchlow (2000: 60) dice que una condición necesaria de este tipo de estructuras es la de cubrir una superficie con polígonos regulares sin dejar espacio entre los puntos de encuentro de sus vértices. La explicación matemática que ofrece para determinar la condición y el número de polígonos regulares es mediante las siguientes fórmulas:
Se toma a «n» como el número de lados del polígono regular. Por lo tanto, el polígono deberá ser un número entero para «n» mayor a 2, por lo que «n» deberá tener valores iguales a 3, 4 ó 6. Las formas regulares que cumplen con esa condición son el triángulo, el cuadrado y el hexágono; con dichos polígonos es posible cubrir un plano bidimensional también de manera regular y equitativa (Critchlow, 2000: 60).
El rango de tres a seis polígonos circundando a un vértice, da 17 posibles soluciones en números enteros (tabla 1). De estas soluciones, solo tres (K, P y S en la tabla 1) pueden ser descontados porque son las ya descritas en las estructuras regulares básicas: la hexagonal, la regular básica y la triangular.
A, B, C, D, F y J también se descuentan porque no proporcionan un patrón continuo para cubrir un plano. De este modo, quedan solo ocho condiciones de encuentro, mismas que dan lugar a otras 14 nuevas estructuras para un total de 22; se tienen así ocho estructuras con particiones que Critchlow (2000) denomina como «semi regulares» y catorce con particiones «demi regulares».
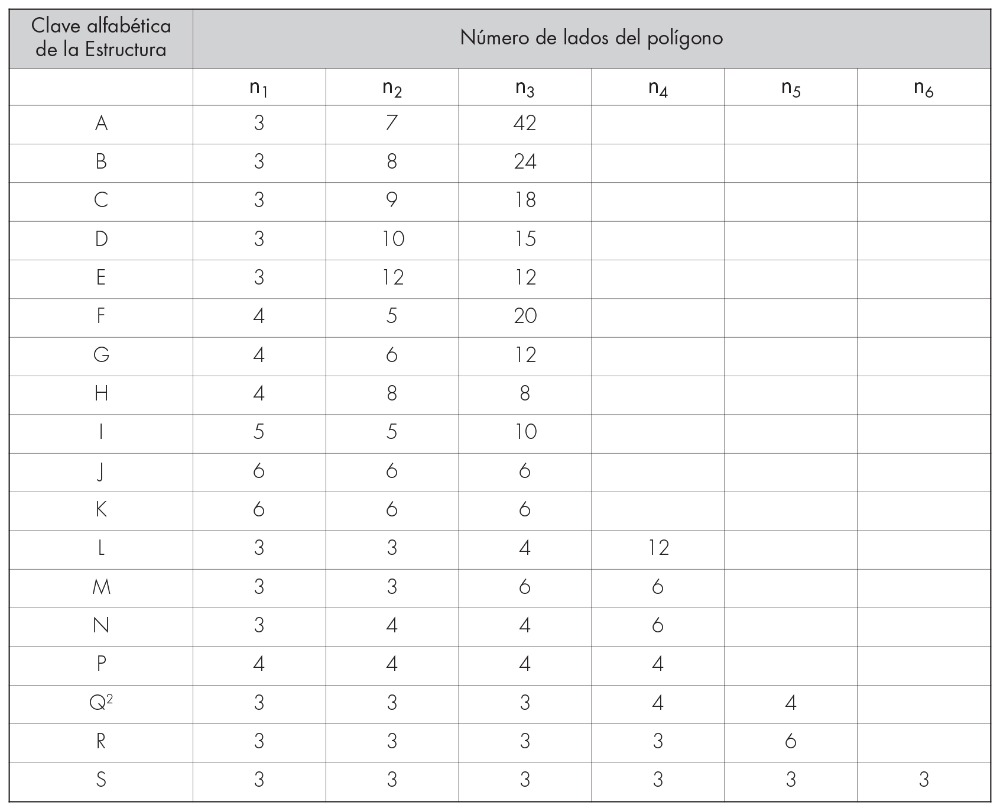
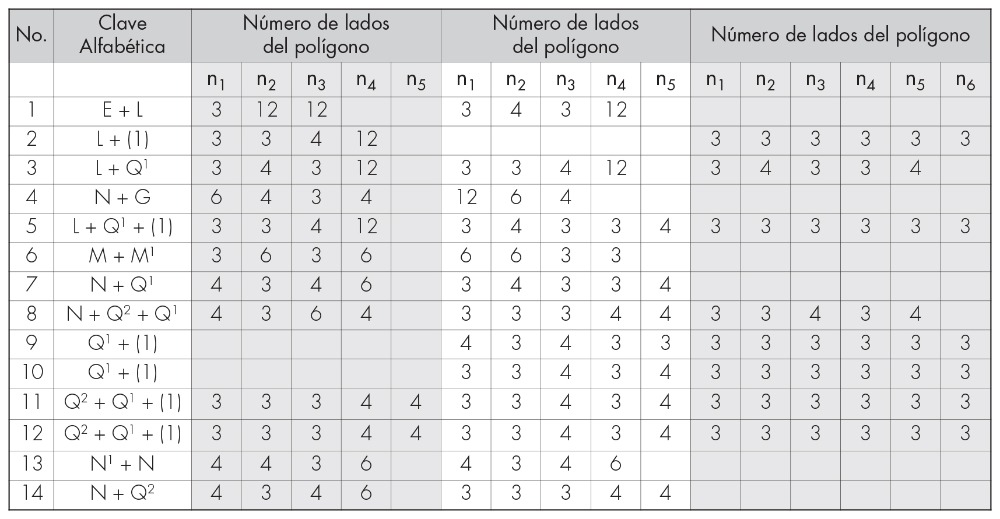
En la tabla 2 se describen las características de las estructuras semi regulares; siete de las ocho combinaciones posibles son empleadas en esta clasificación; la tercera es un arreglo de Q (Q1 y Q2), L aplica solo para estructuras demi regulares:
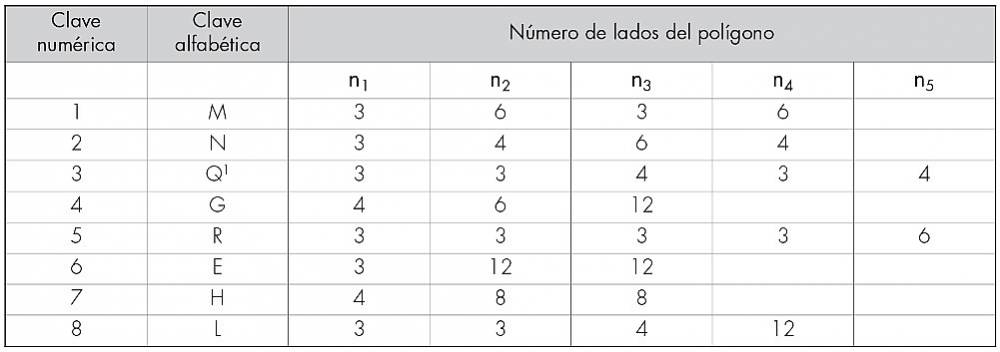
En el siguiente esquema se muestran seis estructuras semi regulares con base en las descripciones de los cuadros anteriores, el acomodo de las formas geométricas se hace con base en la serie numérica obtenida:
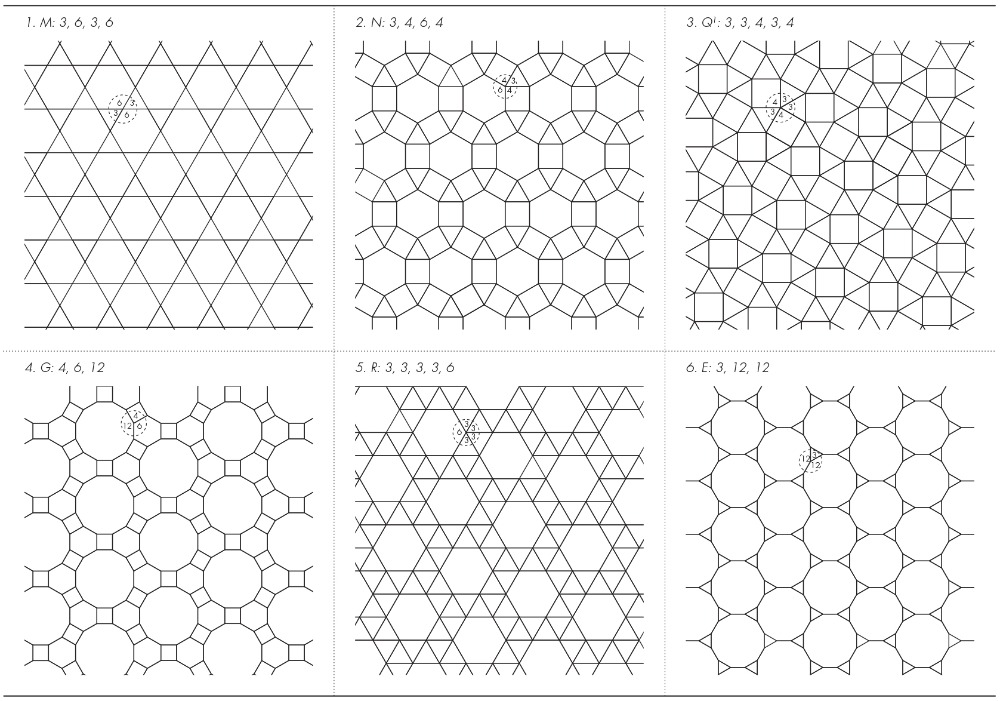
Se muestran catorce estructuras demi regulares de acuerdo con la clasificación de la tabla 3 (Critchlow, 2000). Cinco de estas estructuras (3, 5, 8, 11, 12) presentan tres disposiciones poligonales diferentes en sus vértices.5
Este breve texto ha pretendido mostrar y redescubrir las propuestas geométricas de K. Critchlow, quien logra acertadamente construir un camino que nos puede ayudar a complementar nuestros procesos creativos. Habrá que tomar en cuenta que la labor del diseño se enfoca en la abstracción (geometrización) de lo concreto, y ello podría generar un alejamiento con la realidad en la que pretende intervenir. Una comprensión y diferenciación de los límites del diseño, conceptuales y formales, permitiría relativizar paulatinamente sus posturas (ampliamente discutidas).
¿Qué te pareció? ¡Comparte tu opinión ahora!
- Opiniones:
- 3
- Votos:
- 37
Este video podría interesarte👇👇👇
Colabora con la difusión de este artículo traduciéndolo
Traducir al inglés Traducir al italiano Traducir al portugués- Para mayor detalle de las causas básica cfr. Scott, R., (1970) Fundamentos del diseño. México, Limusa.
- Si un punto se mueve en una sola dirección, de una posición de inicio a otra final, el camino que este punto describe es una línea; Critchlow (2000: 4) denomina a este movimiento primario como la «primera dimensión». Cuando el punto se mueve nuevamente respecto de la posición a la que llegó en el paso anterior, se describe un segundo trazo que dibuja un plano, llamado «segunda dimensión». Si se realiza un tercer trazo por encima del plano descrito en el paso anterior se describe un volumen, denominado a éste último la «tercera dimensión». El volumen tridimensional que se describe en este movimiento del punto es el sólido conocido como Tetraedro, la pirámide de cuatro lados. Para una revisión más detallada cfr. Critchlow, K. (2000) Order In Space. New York, Thames & Hudson.
- La primera referencia que se tiene de estos sólidos es la que hace Platón en el Timeo, de ahí que lleven esta denominación. Cfr. Sutton, D., (2002) Platonic & Archimedean Solids, The Geometry of Space. New York, Wooden Books Ltd.
- A las estructuras formales, Wong (2004) las subdivide en Estructuras Formales de Repetición, Estructuras Formales de Gradación y Estructuras Formales de Radiación. Para mayor destalle, cfr. Wong, W., (2004) Fundamentos del diseño. Barcelona, Gustavo Gili.
- Sin embargo, pueden ser construidas más de veinte estructuras demi regulares modificando la combinación y posición de los vértices de los polígonos que las conforman. Estas estructuras han sido encontradas como patrones de diseño en varias manifestaciones artísticas y religiosas, principalmente en el arte celta e islámico, además de aparecer en varias formaciones naturales y composiciones celulares. Para una revisión más detallada cfr. Critchlow, K. (2000) Order In Space. New York, Thames & Hudson y Lundy, M., (2007). The essential pocket guide to the ancient art of Sacred Geometry. U. S., Wooden Books.
Bibliografía
- Bachelard, G., (1991) La formación del espíritu científico. Contribución a un psicoanálisis del conocimiento objetivo. 2ª. Ed., México, Siglo XXI.
- Critchlow, K. (2000) Order In Space. New York, Thames & Hudson.
- Dondis, D., (2008) La sintaxis de la imagen; introducción al alfabeto visual. Barcelona, Gustavo Gili.
- Lundy, M., (2007). The essential pocket guide to the ancient art of Sacred Geometry. U. S., Wooden Books.
- Margolin, V., (1999) «La construcción de una comunidad de investigación de diseño» en Salinas, O., (Comp.) (2001), Antología de diseño 1. México, Designio.
- Scott, R., (1970) Fundamentos del diseño. México, Limusa.
- Wong, W., (2004) Fundamentos del diseño. Barcelona, Gustavo Gili.
- Sutton, D., (2002) Platonic & Archimedean Solids, The Geometry of Space. New York, Wooden Books Ltd.
Este artículo no expresa la opinión de los editores y responsables de FOROALFA, quienes no asumen responsabilidad alguna por su autoría y naturaleza. Para reproducirlo, salvo que estuviera expresamente indicado, por favor solicitar autorización al autor. Dada la gratuidad de este sitio y la condición hiper-textual del medio, agradeceremos evitar la reproducción total en otros sitios Web.
